2401. Обход в ширину

Задан неориентированный граф. Найдите кратчайшее расстояние между двумя заданными вершинами.

Вход. В первой строке содержится три натуральных числа n, s и f (1 ≤ s, f ≤ n ≤ 100) – количество вершин в графе и номера начальной и конечной вершины. Далее в n строках задана матрица смежности графа. Если значение в j-м элементе i-й строки равно 1, то в графе есть направленное ребро из вершины i в вершину j.

Выход. Выведите минимальное расстояние от начальной вершины до конечной. Если пути не существует, то выведите 0.

Пример входа	Пример выхода
4 4 3 0 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0	2

РЕШЕНИЕ

поиск в ширину

Анализ алгоритма

Кратчайший путь в графе от s до f ищем при помощи поиска в ширину.

Пример

Граф приведенный в примере имеет вид:

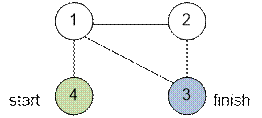
Реализация алгоритма

Объявим матрицу смежности g для хранения графа, а также массив dist для хранения кратчайших расстояний от истока до вершин.

#define MAX 101

int g[MAX][MAX], dist[MAX];

Функция bfs реализует поиск в ширину из вершины start.

void bfs(int start)

{

Инициализируем массив dist. Если dist[i] = -1, то вершина i еще не посещена.

memset(dist, -1, sizeof(dist));

dist[start] = 0;

Объявляем и инициализируем очередь q.

queue<int> q;

q.push(start);

Продолжаем поиск в ширину пока очередь не пустая.

while (!q.empty())

{

Извлекаем и удаляем вершину v из головы очереди.

int v = q.front(); q.pop();

Куда можно пойти из вершины v? Перебираем ребра v → to.

for (int to = 1; to <= n; to++)

Если из v имеется ребро в to, и при этом вершина to еще не пройдена, то идем в нее (ребро (v, to) является ребром дерева при поиске в ширину).

if (g[v][to] && dist[to] == -1)

{

Заносим вершину to в конец очереди. Вычисляем кратчайшее расстояние dist[to].

q.push(to);

dist[to] = dist[v] + 1;

}

}

}

Основная часть программы. Читаем входные данные.

scanf("%d %d %d", &n, &s, &f);

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

scanf("%d", &g[i][j]);

Запускаем поиск в ширину из вершины s.

bfs(s);

Выводим кратчайшее расстояние. Если пути до вершины f не существует (dist[f] < 0), то устанавливаем dist[f] = 0.

if (dist[f] < 0) dist[f] = 0;

printf("%d\n", dist[f]);

Реализация алгоритма – список смежности

Объявим список смежности g для хранения графа, а также массив dist для хранения кратчайших расстояний от истока до вершин.

vector<vector<int> > g;

vector<int> dist;

Функция bfs реализует поиск в ширину из вершины start.

void bfs(int start)

{

Инициализируем массив dist. Если dist[i] = -1, то вершина i еще не посещена.

dist = vector<int>(n + 1, -1);

dist[start] = 0;

Объявляем и инициализируем очередь q.

queue<int> q;

q.push(start);

Продолжаем поиск в ширину пока очередь не пустая.

while (!q.empty())

{

Извлекаем и удаляем вершину v из головы очереди.

int v = q.front(); q.pop();

Куда можно пойти из вершины v? Перебираем ребра v → to.

for (int to : g[v])

Если вершина to еще не пройдена, то идем в нее (ребро (v, to) является ребром дерева при поиске в ширину).

if (dist[to] == -1)

{

Заносим вершину to в конец очереди. Вычисляем кратчайшее расстояние dist[to].

q.push(to);

dist[to] = dist[v] + 1;

}

}

}

Основная часть программы. Читаем входные данные.

scanf("%d %d %d", &n, &s, &f);

g.resize(n + 1);

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

{

scanf("%d", &val);

if (val == 1) g[i].push_back(j);

}

Запускаем поиск в ширину из вершины s.

bfs(s);

Выводим кратчайшее расстояние. Если пути до вершины f не существует (dist[f] < 0), то устанавливаем dist[f] = 0.

if (dist[f] < 0) dist[f] = 0;

printf("%d\n", dist[f]);

Реализация алгоритма – моделирование очереди

Объявим матрицу смежности g для хранения графа, а также массив dist для хранения кратчайших расстояний от истока до вершин.

#define MAX 110

int g[MAX][MAX], dist[MAX];

Функция bfs реализует поиск в ширину из вершины start.

void bfs(int start)

{

Инициализируем массив dist. Если dist[i] = -1, то вершина i еще не посещена.

memset(dist,-1,sizeof(dist));

dist[start] = 0;

Инициализация очереди. Очередь реализуем в виде локального массива q размера MAX (в любой момент времени количество вершин в очереди будет не больше чем количество вершин в графе). Head и Tail – указатели на голову и конец очереди.

int q[MAX], Head = 0, Tail = 1;

q[Head] = start;

Продолжаем поиск в ширину пока очередь не пустая.

while(Head < Tail)

{

Извлекаем вершину v из головы очереди.

int v = q[Head++];

Куда можно пойти из вершины v? Перебираем ребра v → i.

for(int i = 1; i <= n; i++)

Если из v имеется ребро в i, и при этом вершина i еще не пройдена, то идем в нее (ребро (v, i) является ребром дерева при поиске в ширину).

if (g[v][i] && dist[i] == -1)

{

Заносим вершину i в конец очереди. Вычисляем кратчайшее расстояние dist[i].

q[Tail++] = i;

dist[i] = dist[v] + 1;

}

}

}

Основная часть программы. Читаем входные данные.

scanf("%d %d %d",&n,&s,&f);

for(i = 1; i <= n; i++)

for(j = 1; j <= n; j++)

scanf("%d",&g[i][j]);

Запускаем поиск в ширину из вершины s.

bfs(s);

Выводим кратчайшее расстояние. Если пути до вершины f не существует (dist[f] < 0), то устанавливаем dist[f] = 0.

if (dist[f] < 0) dist[f] = 0;

printf("%d\n",dist[f]);

Java реализация – матрица смежности

import java.util.*;

public class Main

{

static int g[][], dist[];

static int n, s, f;

static void bfs(int start)

{

Arrays.fill(dist,-1);

dist[start] = 0;

Queue<Integer> q = new LinkedList<Integer>();

q.add(start);

while(!q.isEmpty())

{

int v = q.poll();

for(int to = 1; to <= n; to++)

if (g[v][to] == 1 && dist[to] == -1)

{

q.add(to);

dist[to] = dist[v] + 1;

}

}

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextInt();

s = con.nextInt();

f = con.nextInt();

g = new int[n+1][n+1];

dist = new int[n+1];

for (int i = 1; i <= n; i++)

for (int j = 1; j <= n; j++)

g[i][j] = con.nextInt();

bfs(s);

if (dist[f] < 0) dist[f] = 0;

System.out.println(dist[f]);

con.close();

}

}

Java реализация – список смежности

import java.util.*;

public class Main

{

static ArrayList<Integer>[] g;

static int dist[];

static void bfs(int start)

{

Arrays.fill(dist,-1);

dist[start] = 0;

Queue<Integer> q = new LinkedList<Integer>();

q.add(start);

while(!q.isEmpty())

{

int v = q.poll();

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v].get(i);

if (dist[to] == -1)

{

q.add(to);

dist[to] = dist[v] + 1;

}

}

}

}

@SuppressWarnings("unchecked")

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int s = con.nextInt();

int f = con.nextInt();

g = new ArrayList[n+1];

for(int i = 0; i <= n; i++)

g[i] = new ArrayList<Integer>();

dist = new int[n+1];

for (int i = 1; i <= n; i++)

for (int j = 1; j <= n; j++)

{

int val = con.nextInt();

if (val == 1) g[i].add(j);

}

bfs(s);

if (dist[f] < 0) dist[f] = 0;

System.out.println(dist[f]);

con.close();

}

}

Python реализация – матрица смежности

Импортируем двустороннюю очередь.

from collections import deque

Функция bfs реализует поиск в ширину из вершины start.

def bfs(start):

Инициализируем глобальный список dist. Если dist[i] = -1, то вершина i еще не посещена.

global dist

dist = [-1] * (n + 1)

dist[start] = 0

Объявляем и инициализируем очередь q.

q = deque([start])

Продолжаем поиск в ширину пока очередь не пустая.

while q:

Извлекаем и удаляем вершину v из головы очереди.

v = q.popleft()

Куда можно пойти из вершины v? Перебираем ребра v → to.

for to in range(1, n + 1):

Если из v имеется ребро в to, и при этом вершина to еще не пройдена, то идем в нее (ребро (v, to) является ребром дерева при поиске в ширину).

if g[v][to] == 1 and dist[to] == -1:

Заносим вершину to в конец очереди. Вычисляем кратчайшее расстояние dist[to].

q.append(to)

dist[to] = dist[v] + 1

Основная часть программы. Читаем входные данные.

n, s, f = map(int, input().split())

g = [[] for _ in range(n + 1)]

for i in range(1, n + 1):

g[i] = [0] + list(map(int, input().split()))

Запускаем поиск в ширину из вершины s.

bfs(s)

Выводим кратчайшее расстояние. Если пути до вершины f не существует (dist[f] < 0), то устанавливаем dist[f] = 0.

if dist[f] < 0: dist[f] = 0

print(dist[f])

Python реализация – список смежности

Импортируем двустороннюю очередь.

from collections import deque

Функция bfs реализует поиск в ширину из вершины start.

def bfs(start):

Инициализируем глобальный список dist. Если dist[i] = -1, то вершина i еще не посещена.

global dist

dist = [-1] * (n + 1)

dist[start] = 0

Объявляем и инициализируем очередь q.

q = deque([start])

Продолжаем поиск в ширину пока очередь не пустая.

while q:

Извлекаем и удаляем вершину v из головы очереди.

v = q.popleft()

Куда можно пойти из вершины v? Перебираем ребра v → to.

for to in g[v]:

Если вершина to еще не пройдена, то идем в нее (ребро (v, to) является ребром дерева при поиске в ширину).

if dist[to] == -1:

Заносим вершину to в конец очереди. Вычисляем кратчайшее расстояние dist[to].

q.append(to)

dist[to] = dist[v] + 1

Основная часть программы. Читаем входные данные.

n, s, f = map(int, input().split())

Инициализируем и строим список смежности g.

g = [[] for _ in range(n + 1)]

for i in range(1, n + 1):

row = [0] + list(map(int, input().split()))

for j in range(1, n + 1):

if row[j] == 1: g[i].append(j)

Запускаем поиск в ширину из вершины s.

bfs(s)

Выводим кратчайшее расстояние. Если пути до вершины f не существует (dist[f] < 0), то устанавливаем dist[f] = 0.

if dist[f] < 0: dist[f] = 0

print(dist[f])